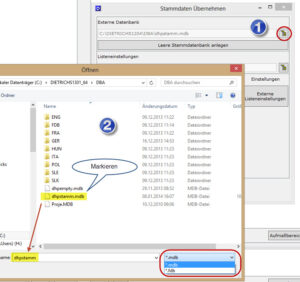
Die Eingabedaten
Es soll eine Liste mit Spundschalung optimiert werden. Die Plattenliste sieht so aus:
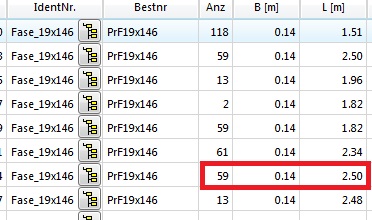
Die Bretter haben also eine Länge zwischen ca. 1,50 m und 2.50 m.
In den Optimierungseinstellungen wird festgelegt welche Blöcke zur Verfügung stehen:
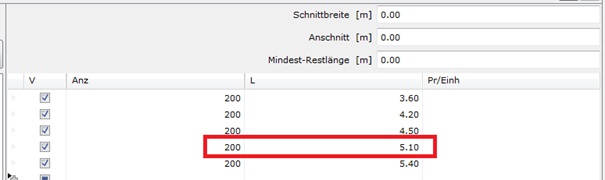
Der Händler hat offensichtlich Schalung von 3,60 m bis 5,40 m Blocklänge auf Lager. Der Preis spielt keine Rolle, um Sägeblattbreiten und Restlängen kümmern wir uns nicht. Die eingegebene Anzahl von 200 signalisiert, dass von jeder Länge ausreichend Bretter beim Händler liegen.
Das unerwartete Ergebnis
Wenn man sich das bildlich vorstellt, fällt z. B. auf: die 59 Bretter von 2,50 m Länge passen doch optimal in den 5,10 m Block. Zwei Bretter pro Block und nur ganz wenig Abfall. Doch was passiert tatsächlich?

Der Computer nimmt die offenkundig ungünstige Blocklänge von 3,60 m her und erzeugt damit einen ganz ansehnlichen Stapel von 1,10 m langen Brettern fürs Feuerholz.
Die Probleme
Haben wir jetzt den Beweis gefunden, dass der Computer dem menschlichen Verstand noch lange unterlegen sein wird? Nein, in den oben geschilderten Annahmen verstecken sich zwei Missverständnisse.
Mindest-Restlänge
Viele Benutzer denken, dass die Mindest-Restlänge lediglich Einfluss auf die Ausgabe hat. So kann man z. B. sagen, dass alles unter einem Meter tatsächlich Verschnitt (Feuerholz) ist und alles darüber kann man noch gebrauchen und aufheben. Das stimmt so weit, ist aber noch nicht alles.
Im obigen Beispiel ist die Mindest-Restlänge 0,00 m. Das bedeutet: Es wird kein Verschnitt herauskommen. Wenn bereits 1 mm übrig bleibt wird davon ausgegangen, dass es sich um einen Rest handelt. Und ein Rest kann noch anderweitig verwendet werden. Der Algorithmus versucht in erster Linie, den Verschnitt klein zu halten, Reste sieht er als nicht so problematisch an. Daher kann es sein, dass ein offenkundig ungünstiges Ergebnis rauskommt.
Daher der Tipp: Wenn nicht mit Resten gearbeitet wird, einen möglichst großen Wert (z. B. Mindest-Restlänge 100 m) eingeben. Dann wird auf jeden Fall versucht den Verschnitt möglichst klein zu halten.
Im obigen Beispiel wurde dieser Lösungsansatz ausprobiert. Um es gleich zu sagen, das Ergebnis war identisch. Statt insgesamt 305 m Rest sind nun 305 m Verschnitt rausgekommen. Immer noch wurde ein Brett von 2,50 aus einem Block von 3,60 herausgeschnitten.
Funktionsweise der Anzahl
Das zweite Missverständnis ist die Eingabe der Anzahl. Die Absicht war wohl: „Mit 200 Brettern ist von jeder Länge genug da.“ Die Optimierung versteht aber: „Von den jeweiligen Längen liegen noch 200 Stück rum, mach die erst mal weg.“
Wenn eine Anzahl eingegeben ist, geht der Algorithmus davon aus, dass das Resthölzer sind, die noch rumliegen und damit bevorzugt zu verwenden sind. Und welche nimmt er sich zuerst vor? Natürlich die Kürzesten. Das sieht man auch in der Ergebnisliste:
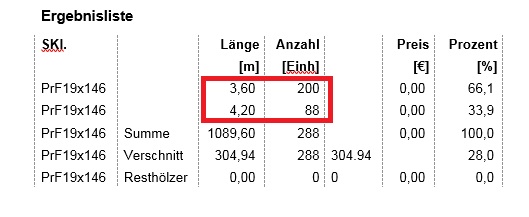
Diese 200 kurzen Restbretter von 3,60 m sind jetzt endlich weg. Es mussten noch 88 längere Bretter verwendet werden.
Also: Wenn eine Anzahl eingegeben ist, wird davon ausgegangen, dass das Reste sind, die zuerst verarbeitet werden sollen. Dann wird mit den Kürzesten begonnen.
Das gewünschte Ergebnis
Wenn ich die Anzahl ganz rausnehme und die Mindest-Restlänge auf 100,00 m stelle sehe ich, dass die Optimierung für meine 2,50 m Bretter noch eine andere Lösung gefunden hat:

Vermutlich ist es also insgesamt günstiger, gar nicht 2 mal 2,50 in einen 5,10 m Block zu legen, sondern jeweils ein Brett von 1,51 m und 2,50 m aus einem 4,20 m Block zu schneiden. Ob das tatsächlich optimaler ist? Ich werde mir nicht die Mühe machen es auszuprobieren, für so eine Fleißarbeit habe ich ja den Computer.
Das Gesamtergebnis sieht auf jeden Fall sehr viel günstiger aus:
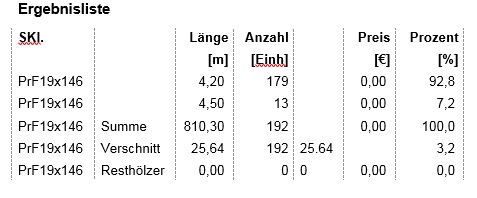
Der Verschnitt wurde ca. um den Faktor 12 reduziert.